The WaLK Lab

Problem: What height did the rocket attain? What was the average velocity of the rocket? What was the value of the force of air resistance and drag?

Materials: - rocket

- launch pad

- device to measure angular distance

Procedure:

1. Build rocket.
2. Record the mass of the empty rocket (without the engine).
3. Insert the engine and record the mass of the rocket before the launch.
4. Have two trackers walk out opposite each other a set distance from the launch pad (baseline) so that they are both situated in a line to the launch pad that is perpendicular to the direction of the wind. Once the rocket is launched these trackers should record the change in elevation as the rocket travels from launch to apogee (angular distance).
5. Have someone ready to record the total time of the launch, the time taken to attain apogee, and the time at which the deployment system is released.
6. Launch rocket.
7. Collect the rocket and record all data.
8. Record the mass of the rocket after launch.

Data:

Rocket:

Diameter: 4.0 cm

Engine: B6-4

Total Impulse: B à 2.500-5.000 à 3.750 Newton-seconds

Average Thrust: 6 N

Delay Time: 4”

Launch details:

Location: Dundonald Park, Saskatoon

Time: 12:45 pm, Sunday November 13, 2005

Wind: S 17 km/h

Other launches: Two other launches had been conducted previously but results were inaccurate and inconclusive

Collected data:

Mass of engine: 18.5 g

Mass of empty rocket: 80.0 g

Mass before launch: 98.5 g

Mass after launch: 90.5 g

Total time of launch: 16.62 s

Launch to apogee: 4.53 s

Therefore, apogee to landing: 16.62 – 4.53 = 12.09 s

Parachute deployed: 7.35 s

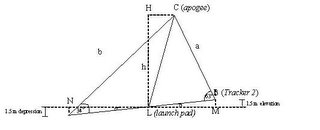
Angular distance: Two tracker system: 34º and 63º

Baseline: 300 feet = 91.44 meters = 90 meters

Tracker 1 at 2 m depression from launch pad elevation

Tracker 2 at 2 m elevation from launch pad elevation

Analysis:

Rocket Equations

Using the Rocket Equations Quick Reference Sheet (See attached or http://my.execpc.com/~culp/rockets/qref.html), a Delphi program was created using those equations to calculate the following values:

Input Data:

Mass of empty rocket: 0.0800 kg

Mass of rocket before launch: 0.0985 kg

Mass of rocket after launch: 0.0905 kg

Motor thrust: 6 N

Motor impulse: 5 Newton-seconds

Rocket Radius: 0.020 m

Output Data:

Average mass during boost: 0.0945 kg

Mass during coast: 0.0905 kg

Rocket cross sectional area: 0.0013 m²

Motor burn time: 0.83 s
Burnout velocity: 42 m/s
Altitude at burnout: 18 m
Coasting distance: 59 m

Peak altitude (apogee): 77 m
Coasting time: 3.7 s

Other values:

k: 0.00057491097
q: 93.9355985817249
x: 1.14295462641588
q_a: 39.296918440565
q_b: 0.249637895012995

Altitude (h) :

For ∆ ANL

NL = 90

AN = 1.5

c² = a² + b²

(AL)² = (AN)² + (NL)²

8102.25 = (1.5)² + (90)²

c = AL = 90.0139

c = 90 m

tan(Angle ALN) = AN/NL

Angle ALN = tan^-1(AN/NL)

= tan^-1(1.5/90)

= tan^-1(0.01666667)

Angle ALN = 0.9548º

For ∆ BML

ML = 90

BM = 1.5

c² = a² + b²

(BL)² = (BM)² + (ML)²

8102.25 = (1.5)² + (90)²

c = BL = 90.0139

c = 90 m

Angle ALN = Angle BLM

Angle BLM = 0.9548º

Therefore, AB = AL + BL = 90 + 90

AB = 180 m

In ∆ ABC, Angle C = 180- Angle A - Angle B

= 180 - 34 - 63

= 83º

Using the Law of Sines for ∆ ABC:

a/sin(A) = b/sin(B) = c/sin(C)

a/sin(34º) = b/sin(63º) = 180/sin(83º)

a/0.559 = b/0.891 = 180/0.993

Therefore:

a = [(180)(0.559)]/0.993

a = 101.4263 = 1 x 10² m

b = [(180)(0.891)]/0.993

b = 161.6107 = 160 m

Using the Law of Cosines for ∆ ACL

c² = a² + b² - 2ab*cos(C)

(CL)² = 90.0139² + 161.6107² – 2(90.0139)(161.6107)*cos(34º)

(CL)² = 10100.1542

CL = 100.4995 m

CL = 100 m

Using the Law of Cosines for ∆ BCL

c² = a² + b² - 2ab*cos(C)

(CL)² = 90.0139² + 101.4263² – 2(90.0139)(101.4263)*cos(63º)

(CL)² = 10100.13264

CL = 100.4994 m

CL = 100 m

Using the Law of Sines for ∆ ACL:

a/sin(A) = b/sin(B)

b/sin(Angle ALC) = CL/sin(Angle A)

161.6/sin(Angle ALC)= 100.5/sin(34º)

sin(Angle ALC) = [sin(34º)*161.6]/100.5

= 0.8992

Angle ALC = 115.9438º

Angle ALC = 116º à 120º

For ∆ LCH

Angle HLC = Angle ALC – Angle NLA - 90º

= 115.9438 – 0.9548 – 90

= 24.989º

= 25º

To find h:

cos(Angle HLC) = h/CL

cos(24.989) = h/100.5

h = 100.5*cos(24.989)

h = 91.0921

h = 91 m

h = 90 m (choosing only 1 significant figure)

Average speed:

Average speed = (distance traveled)/(time)

Average speed ascending = 90/4.53

= 19.9 m/s

Average speed descending = -90/12.09

= -7.44 m/s

Force Analysis

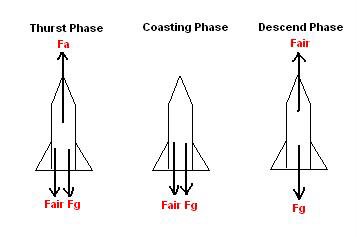
Thrust Phase:

F_net = ma = F_air + F_g + F_a

m = (98.5 + 90.5)/2

= 94.5 g à 0.0945 kg

v₂ = average speed ascending x 2

= 19.9 x 2 = 39.8 m/s

a = (v₁ + v₂)/burn time

a = (0 + 39.8)/ 0.83 = 47.95

= 48 m/s²

F_g = mg

= 0.0945 (- 9.8)

= - 0.93 N

F_a = 6

F_net = ma = F_air + F_g + F_a

(0.0945)(48) = F_air - 0.93 + 6

4.536 = F_air + 5.07

F_air = - 0.534

F_air = - 0.53 N

Coasting Phase:

F_net = ma = F_air + F_g

m = 90.5 g à 0.0905 kg

a = - (v₁ + v₂)/(time - burn time)

a = - (39.8 + 0)/ (4.53 – 0.83)

a = - 10.8 m/s²

F_g = 0.0905(- 9.8)

= - 0.89 N

F_net = ma = F_air + F_g

(0.0905)(- 10.8) = F_air - 0.89

- 0.97374 = F_air - 0.89

F_air = - 0.0874

F_air = - 0.087 N

Descent Phase:

F_net = ma = F_air + F_g

F_net = ma = F_air + F_g

(0.0905)(-7.44) = F_air - 0.89

-0.67360 = F_air - 0.89

F_air = 0.21630

F_air = 0.22 N

Sources of Error:

Possible sources of error include:

- Inaccurate measurements of the angular distance due to human error

- Inaccurate measurement of the baseline

- Inaccurate measurement of the depression and elevation in terrain

- Timing inaccuracies

- Imperfections in flight path due to weather conditions or angle of launch

- Incomplete burn time and thus leftover burn mass

- Estimation of v₁ and v₂ (especially for the descent phase as the rocket probably attained terminal velocity before landing)

It is significant to note that while the rocket launch was successful, it is difficult to come to concrete conclude based on the results of one rocket launch because there are so many contributing and varying factors, such as the changing wind speed and direction.

Conclusion:

The altitude attained by the rocket was 90 meters. The average speed ascending was 19.9 m/s, and the average speed descending was -7.44 m/s.

During the thrust phase of the rocket launch the force of drag (or air resistance) was - 0.53 N, acting with the force of gravity to slow the rocket down as it accelerated upwards. During the coasting phase the force of drag was - 0.087 N, acting with the force of gravity to slow the rocket down until there was no more acceleration. Finally during the descent phase the force of drag was 0.22 N, acting against gravity to slow the descent of the rocket and thus slow the acceleration downwards.